Question

How much work in joules is done on the system when a 1.15 atm external pressure causes a piston to decrease in volume in volume from 6.55 Liters to 3.16 Liters ?

Answer 1

We have according to the statement a gas to which external pressure is exerted to reduce its volume. We will first assume that the process occurs at a constant temperature and pressure. The work done by that external force is determined by the following form of work (W):

`W=-P*\Delta V`
`W=-P*(V_2-V_1)`

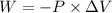
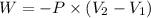
Where,

P is the external pressure, 1.15atm

V2 is the final volume, 3.16L

V1 is the initial volume, 6.55L

We replace the known values:

`\begin{gathered} W=-1.15atm*(3.16L-6.55L) \\ W=3.8985atm/L \end{gathered}`

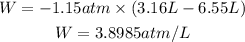
We will convert these units to joules. 1atm/L=101.325J.

`W=3.8985atm/L*(101.325J)/(1atm/L)=395J`

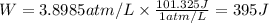
Answer: The work in joules done is 395 J