Question

I need help I’ve been trying these for so long

Answer 1

We know that all the three parts are straight lines, and we know that the equation or the function that represents this straight lines is

`f(x)=m\cdot x+b\text{ or }y=m\cdot x+b`

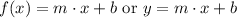
For straight lines we have at least two points so we can find their functions.

For the first one on the left side, we have the points (-5,2) and (-3,-1), first we find the slope (m)

`m=(-1-2)/(-3-(-5))=(-3)/(-3+5)=-(3)/(2)`

So, we have the first piece to finding the function of this line, and we can fill it into f(x) =mx+b like this

`f(x)=-(3)/(2)x+b`

To find b, think about what your (x,y) points mean:

(-5,2). When x of the line is -5, y of the line must be 2.

(-3,-1). When x of the line is -3, y of the line must be -1.

Because you said the line passes through each one of these two points, right?

Now, look at our line's equation so far: y=-3/2x+b. b is what we want, the -3/2 is already set and x and y are just two "free variables" sitting there. We can plug anything we want in for x and y here, but we want the equation for the line that specfically passes through the two points (-5,2) and (-3,-1).

So, why not plug in for x and y from one of our (x,y) points that we know the line passes through? This will allow us to solve for b for the particular line that passes through the two points you gave!.

You can use either (x,y) point we want..the answer will be the same. we replace the two points in the equation, taking in count that y=f(x), we have for (-5,2) that

`\begin{gathered} 2=-(3)/(2)(-5)+b \\ 2=(15)/(2)+b \\ 2-(15)/(2)=b \\ -(11)/(2)=b \end{gathered}`

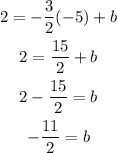
and for (-3, -1)

`\begin{gathered} -1=-(3)/(2)(-3)+b \\ -1=(9)/(2)+b \\ -1-(9)/(2)=b \\ -(11)/(2)=b \end{gathered}`

The first function is

`f(x)=-(3)/(2)x-(11)/(2)`

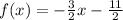
Doing the same process for the third function (the first function on the rigth side), we can find the function with the points (2,-3) and (6,1)