Question

Two similar triangles have a pair of corresponding sides of length 12 meters and 8 meters. The larger triangle has a perimeter of 48 meter. Find the perimeter of the smaller triangle Two similar triangles have a pair of corresponding sides of length 12 meters and 8 meters. The larger triangle has an area of 180 square meters. Find the area of the smaller triangle.

Answer 1

Given data:

The side of the first triangle is x= 12 meter.

The side of the second triangle is y=8 meter.

The perimeter of the first triangle is P= 48 meter.

The expression for the ratio of the similar triangle,

`\begin{gathered} (x)/(y)=(P)/(p) \\ \frac{12\text{ m}}{8\text{ m}}=\frac{48\text{ m}}{p} \\ p=48\text{ m(}(8)/(12)) \\ =32\text{ m} \end{gathered}`

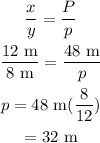
The expression for the area is,

`\begin{gathered} (x^2)/(y^2)=(A)/(a) \\ ((12m)^2)/((8m)^2)=(180m^2)/(a) \\ a=(1)/(2.25)*180m^2 \\ =80m^2 \end{gathered}`

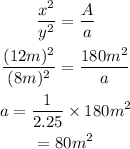
Thus, the perimeter of the smaller triangle is 32 m, and the area of the smaller triangle is 80 square-meter.