Step-by-step explanation:
The function is given below as
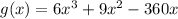
To find g'(x) , we will have
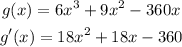
Hence,
The final answer is
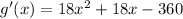
Part 2:
Find g''(x)
To find g''(x) we will so the calculation below
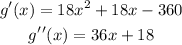
Hence,
The final answer is
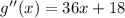
Part 3:
Evaluate g''(-5)
To do this, we will put x= -5 in g''(x)
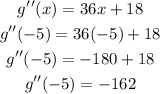
Hence,
The final answer is
![g^{\operatorname{\prime}\operatorname{\prime}}(-5)=-162]()