We are asked to prove the congruency of the triangles GFM and BCM. To prove congruency we initially prove that angles:
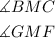
Are congruent by the vertical angles theorem.
Also, since segments CB and FG are parallel, this means that:

This is by alternate interior angles theorem.
Finally, the congruency is proven by ASA (Angle Side Angle) since we have two congruent pairs of angles and we are given that sides CM and MF are congruent. Therefore, the triangles are congruent.