Answer:
104.5 feet
Explanation:
Given a basketball court in the shape of a rectangle with the following dimensions:
• Length = 94 feet
,
• Width = 50 feet
The diagonal of the rectangle divides the rectangle into two right triangles as shown in the diagram below:
The length of the diagonal forms the hypotenuse of each of the right triangles.
Using Pythagoras' theorem, we find the value of the hypotenuse labeled x above:
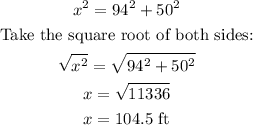
The length of the diagonal of the court is 104.5 feet (rounded to the nearest tenth).
own in