Question

I need to know the measure of angle C in the image attached

Answer 1

Considering the quadrilateral ABCD

The sides AB and BC are equal, as well as sides AD and .

Thanks to these sides being equal, angles ∠A and ∠C are also equal.

If you draw a line from A to C two isosceles triangles will be determined:

ΔABC and ΔACD

ΔABC

AB = BC → the triangle is isosceles, then the base angles are equal:

∠BAC = ∠BCA

ΔACD

AD = DC → the triangle is isosceles, then the base angles are equal

∠DAC = ∠DCA

Applying the angle addition postulate we can determine that:

Angle C is equal to the sum of ∠BCA and ∠ DCA

`\angle C=\angle\text{BCA}+\angle\text{DCA}`

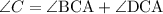
Angle A is equal to the sum of ∠BAC and ∠DAC

`\angle A=\angle\text{BAC+}\angle DAC`

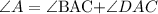
Then, by the transitive property of equality, we can conclude that:

`\angle C=\angle A`

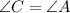
Now, the sum of the inner angles of a quadrilateral is 360º, then:

`\angle A+\angle B+\angle C+\angle D=360º`

Let "x" represent the measure od ∠A and ∠C, we know that ∠B=117º and ∠D=70º

`x+117º+x+70º=360º`

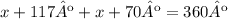
From this expression you can determine the value of x:

- Simplify the like terms:

`\begin{gathered} x+117º+x+70º=360º \\ x+x+117º+70º=360º \\ 2x+187º=360º \end{gathered}`

- Subtract 187º to both sides of the equal sign:

`\begin{gathered} 2x+187º-187º=360º-187º \\ 2x=173º \end{gathered}`

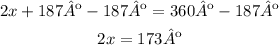
- Divide both sides by 2

`\begin{gathered} (2x)/(2)=(173º)/(2) \\ x=86.5º \end{gathered}`

The measure of ∠C is 86.5º