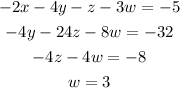
Above are four equations we can use to solve for the values of x, y, z, and w.
Since it is already shown that w = 3, let's solve for "z" using the third equation.
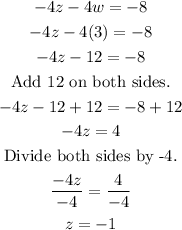
From the above solution, the value of z = -1.
To solve for "y", let's use the second equation and the values of w and z.
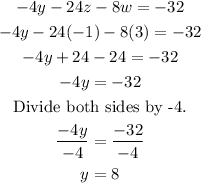
The value of y is 8 as shown above.
Lastly, to solve for "x", let's use the first equation and the values of w, z, and y.
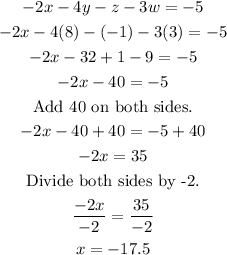
The value of x is -17.5 or -35/2.
To summarize the results, we have:
x = -35/2
y = 8
z = -1
w = 3