Question

Two questions:1. How do I simplify an imaginary number with a coefficient and an exponent For example : 3i^362. How do I simplify an imaginary number equation when there is a radical involved For example 7(-5i + radical -81)

Answer 1

First of all, there are only four possible results for a power of the imaginary unit i: 1, -1, i or -i. These depend on the exponent of the power:

`\begin{gathered} i^(4n)=1 \\ i^(4n+1)=i \\ i^(4n+2)=-1 \\ i^(4n+3)=-i \end{gathered}`

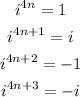
Where n can be any integer equal or greater than 0. So every time you need to simplify a power of i you have to check if its exponent can be written as 4n, 4n+1, 4n+2 or 4n+3. For example if we want to simplify:

`3i^(36)`

We need to equalize 36 to each of the four expressions with n and see for which n is an integer. For example for 4n we have:

`\begin{gathered} 4n=36 \\ n=(36)/(4)=9 \end{gathered}`

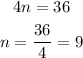
So n is an integer which means that 36 can be written as 4n. If you try with the other 3 expressions you'll see that n is not an integer. Then we have that:

`i^(36)=i^(4n)=1`

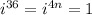
And then you have:

`3i^(36)=3`

When you have a radical like in:

`7\cdot(-5i+\sqrt[]{-81})`

Is important to remember two things:

- The definition of the imaginary unit.

- A property of radicals.

The first one is:

`\sqrt[]{-1}=i`

And the second one is:

`\sqrt[]{xy}=\sqrt[]{x}\cdot\sqrt[]{y}`

Then if you have a negative number inside a radical you can always do the following:

`\sqrt[]{-81}=\sqrt[]{(-1)\cdot81}=\sqrt[]{-1}\cdot\sqrt[]{81}=i\cdot\sqrt[]{81}=i\cdot9`

Then we can simplify the example:

`\begin{gathered} 7\cdot(-5i+\sqrt[]{-81})=-35i+7\sqrt[]{-81} \\ -35i+7\sqrt[]{-81}=-35i+7\cdot i\cdot9 \\ -35i+7\cdot i\cdot9=-35i+63i=28i \end{gathered}`

Then the simplification ends with:

`7\cdot(-5i+\sqrt[]{-81})=28i`