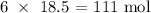Question

2. Consider the reaction: 2C6H4Cl₂ +1302 → 12CO₂ + 2H₂O + 4HC1a.) If you had 18.5 mol of C6H4Cl2, how many mol of CO₂ would you produce?b.) If you had 150.6 mol of O₂, how many mol of CO₂ would you produce?c.) If you had 18.5 mol of C6H4Cl₂ and 150.6 mol of O2, which reactant would be limiting?d.) What is the theoretical yield of CO2, in moles?3. How many grams of H2O would be produced if 20 5 grams H? renot with 80

Answer 1

`\begin{gathered} a)\text{ 111 moles} \\ b)\text{ 139.02 moles} \\ c)\text{ C}_6H_4Cl_2 \\ d)\text{ 111 moles} \end{gathered}`

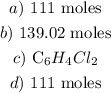
Step-by-step explanation:

a) From the balanced equation of reaction:

2 moles of dichlorobenzene produced 12 moles of carbon dioxide

18.5 moles of dichlorobenzene will produce x moles of carbon dioxide

To get the value of x, we have it that:

`\begin{gathered} 2\text{ }* x\text{ = 18.5 }*12 \\ x\text{ = }(18.5*12)/(2)\text{ = 111 moles} \end{gathered}`

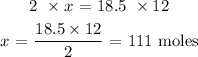
b) From the equation of reaction:

13 moles of oxygen produced 12 moles of carbon dioxide

150.6 moles of oxygen will produce x moles of carbon dioxide

To get the value of x, we have it that:

`\begin{gathered} 13\text{ }*\text{ x = 12 }*150.6 \\ x\text{ = }(12*150.6)/(13) \\ x\text{ = 139.02 moles} \end{gathered}`

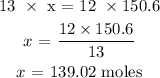
c) The limiting reagent would be the reactant that produces less of the product

dichlorobenzene produces less and thus, it is the limiting reactant

d) To get the theoretical yield, we multiply the number of moles of the limiting reagent by the ratio between the product and the limiting reagent

We have the number of moles of the limiting reagent by the mole ratio

We have the number of moles of the limiting reagent as 18.5 mol and the mole ratio as (product to reactant = 12:2 = 6 to 1)

We have the theoretical yield as:

`6\text{ }*\text{ 18.5 = 111 mol}`