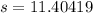1 Answer

Bikash · Answer 1 · 2023-10-01T03:03:53+0000

We need to use the variance and standard deviation for a sample:

The equation for a variance is:

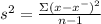
$s^2=(\Sigma(x-x^-)^2)/(n-1)$

Where x⁻ is the mean of x and n is the total number of values.

First, let us find the mean:

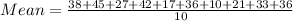
Then :

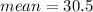
Now, we can find the variance:

$s^2=(\Sigma x-30.5)/(10-1)=((38-30.5)+(45-30.5)+(27-30.5)+(42-30.5)+(17-30.5)+(36-30.5)+(10-30.5)+(21-30.5)+(33-30.5)+(36-30.5))/(9)$

Simplify it:

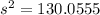
Now, we need to use the next formula to find the standard deviation:

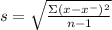
$s=\sqrt{(\Sigma(x-x^-)^2)/(n-1)}$

Then:

$s=\sqrt{((38-30.5)^2+(45-30.5))^2+(27-30.5))^2+(42-30.5))^2+(17-30.5))^2+(36-30.5))^2+(10-30.5))^2+(21-30.5))^2+(33-30.5))^2+(36-30.5))^2)/(9)}$

Then, the standard deviation is:

Please log in or register to add a comment.