Question

A coffee distributor plans to mix some Guatemala Antigua coffee thatnormally sells for $8.30 per pound with some House coffee that normallysells for $10.80 per pound to create 60 pounds of a new coffee blend thatcan sell for $9.76 per pound.How many pounds of each kind of coffee should they mix?

Answer 1

Given:

Antigua coffee sells for $8.30/lb

House coffee sells for $10.80/lb

Let the lb of Antigua coffee and house coffee be x and y respectively.

Since we created 60 lb of the new coffee, we have the relationship:

`x\text{ + y = 60}`

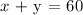
The cost of the new coffee is $ 9.76/lb. We have the relationship:

`\begin{gathered} 8.3x\text{ + 10.8y = 9.76}*60 \\ 8.3x\text{ + }10.8y\text{ = 585.6} \end{gathered}`

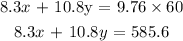
Solving the equations below simultaneously:

`\begin{gathered} x\text{ + y = 60} \\ 8.3x\text{ + 10.8y = 585.6} \end{gathered}`

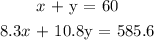
By graphical method:

We notice that the solution to the simultaneous equation is:

(25, 35).

Hence, we can conclude that they should mix 25 lb of Antigua coffee and 35 lb of house coffee.

Answer:

Antigua = 25 lb

House = 35 l