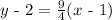Using implicit differentiation, find the equation of the line tangent to the curve below at the point (1 , 2). Leave answer in point-slope form.

Question

asked Apr 1, 2023 81.4k views

1 Answer

Behe · Answer 1 · 2023-04-04T19:33:28+0000

Step-by-step explanation:

Consider the following expression:

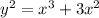
In the first place, we differentiate this expression using implicit differentiation. For this, we treat y as a function of x. Therefore, we get:

$2y\text{ }(dy)/(dx)=3x^2+6x$

solving for dy/dx, we get:

Equation 1:

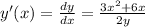
$y^(\prime)(x)=(dy)/(dx)=(3x^2+6x)/(2y)$

Now, remember that the equation of the tangent line is given by the following formula:

Equation 2:

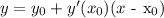
$y=y_0+y^(\prime)(x_0)(x\text{ - x}_0)$

If (x_0 , y_0 ) = (1 , 2), the above equation becomes:

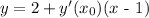
$y=2+y^(\prime)(x_0)(x\text{ - 1})$

Now, applying the equation 1 using the point (x_0 , y_0 ) = (1 , 2), we get the slope of the line at this point:

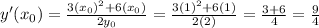
$y^(\prime)(x_0)=(3(x_0)^2+6(x_0))/(2y_0)=(3(1)^2+6(1))/(2(2))=(3+6)/(4)=(9)/(4)$

applying this value in equation 2, we get:

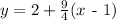
$y=2+(9)/(4)(x\text{ - 1})$

this is equivalent to:

Equation 3:

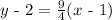
$y\text{ - 2}=(9)/(4)(x\text{ - 1})$

Now, remember that the Point-Slope Form of a Line is given by the following formula:

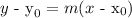
$y\text{ - y}_0=m(x\text{ - x}_0)$

we can see that equation 3 is expressed in that way. Thus, we can conclude that the correct answer is:

Answer:

$y\text{ - 2}=(9)/(4)(x\text{ - 1})$