Question

Prove that secθcotθ = cscθ

Answer 1

In the question, we are asked to prove that

`\sec \theta\cot \theta=\csc \theta`

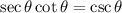
We can find the proof below.

Explanation

To find the proof we must recall some fundamental principles of trigonometry.

`\begin{gathered} 1)\sec \theta=(1)/(\sin \theta) \\ 2)\cot \theta=(\cos \theta)/(\sin \theta) \\ 3)(1)/(\cos\theta)=\csc \theta \end{gathered}`

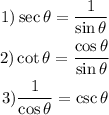
We will then simplify the left-hand side. If it gives the same value as the right-hand side, it implies that the proof is complete.

Therefore, from the left-hand side,

Proof

`\begin{gathered} \sec \theta\cot \theta=(1)/(\cos \theta)*(\cos\theta)/(\sin\theta)=\frac{1}{\text{sin}\theta} \\ =\csc \theta \end{gathered}`

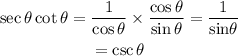
Since the left-hand side has been proven to be equal to the right-hand side when simplified, that concludes the prove