Question

Given vectors = (-6,4) and v=(7, 10), determine if the vectors are orthogonal. If they are not orthogonal, find the angle between the two vectors

Answer 1

The given vectors are:

`\begin{gathered} u=\langle-6,4\rangle \\ v=\langle7,10\rangle \end{gathered}`

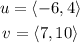
Two vectors are orthogonal if the dot product of the two vectors is zero, let's check:

`\begin{gathered} u\cdot v=(-6)*7+(4*10) \\ u\cdot v=-42+40 \\ u\cdot v=-2 \end{gathered}`

As the product is not zero, then they are not orthogonal.

Now, we need to find the angle between them:

`\cos\theta=(u\cdot v)/(||u||*||v||)`

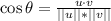
We already know u*v, now, let's find ||u|| and ||v||:

`\begin{gathered} ||u||=√((-6)^2+(4)^2)=√(36+16)=√(52) \\ ||v||=√(7^2+10^2)=√(49+100)=√(149) \end{gathered}`

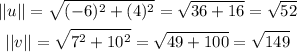
Now, replace these values, and solve for theta:

`\begin{gathered} \cos\theta=(-2)/(√(52)*√(149))=(-2)/(√(7748))=(-2)/(88.02) \\ \cos\theta=-0.023 \\ \theta=\cos^(-1)(-0.023) \\ \theta=91.3\degree \end{gathered}`

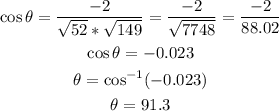
The answer is B. The vectors are not orthogonal. The angle between them is 91.3°