Question

On graph paper, graph the line that goes through the points (-6, 3) and (-3, -1). a. What is the slope of the line?b. What is the intercept?c. Find the equation of the line.

Answer 1

a. Slope = -4/3

b. y-intercept = -5

c. Equation: y = -4/3x -5

Step-by-step explanation:

a.

First, we find the slope of the line connecting the two points

`slope=(\Delta y)/(\Delta x)=(3--1)/(-6+3)=-(4)/(3)`

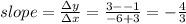
b.

We know that the slope-intercept of a line is

`y=mx+b`

where m is the slope and b is the y-intercept.

Since m = -4/3, we have

`y=-(4)/(3)x+b`

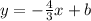
from (-3, -1) we know that when y = -1, x = -3 and so putting these values in the abvoe equation gives

`-1=-(4)/(3)(-3)+b`
`\rightarrow-1=4+b`

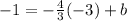
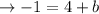
subtracting 4 form both sides gives

`b=-5`

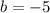
Hence the y-intercept is -5.

c.

The equation of the line is (with m = -4/3 and b = -5)

`y=-(4)/(3)x-5`

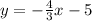
which is our answer!