Given:
The equation of line is given as,
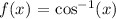
Required:
Equation of tangent line at the point given as,
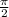
Step-by-step explanation:
The standard form of the equation of tangent line is given as,

Slope of the required tangent line is calculated by taking the derivative of the given function.
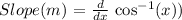
Therefore,
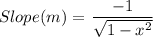
Slope at the given point is calculated as,
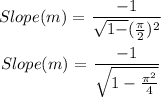
On simplifying further,
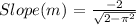
The tangent line passes through the point
![((\pi)/(2),\text{ Undefined \rparen}]()
Therefore the equation of the tangent to the given line is,
![y\text{ = \lbrack}(-2)/(√(2-\pi^2))]x\text{+ undefined}]()
Answer:
Thus the required equation of the tangent line is,
![y=\frac{\text{-2}}{√(2-\pi^2)}x\text{ + undefined}]()