Question

Could you solve this and write it in paragraph form?

Answer 1

The given polynomial function is

`f(x)=-x^3+15x^2-75x+125`

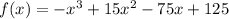
It is a cubic function because the greatest power of x is 3

Since there is no value of x can make f(x) undefined, then

The domain is all real numbers

`D=(-\infty,\infty)`

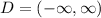
The range is the values of y corresponding to x, then

The range is all the real number

`R=(-\infty,\infty)`

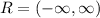
The end of behavior is

Rises to left and falls to the right

The turning point is the point that the tangent to the curve at this point = 0

Then to find it differentiate f(x) and equate it by 0 to get the x-coordinate of it

`\begin{gathered} f^(\prime)(x)=-3x^2+30x-75 \\ f^(\prime)(x)=0 \\ -3x^2+30x-75=0 \\ (-3x^2)/(-3)+(30x)/(-3)-(75)/(-3) \\ x^2-10x+25=0 \\ (x-5)^2=0 \\ x-5=0 \\ x=5 \\ f(5)=-125+375-375-125 \\ f(5)=0 \end{gathered}`

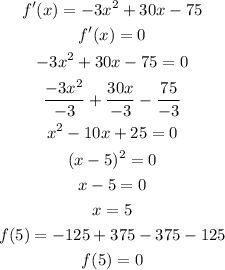
The turning point is (5, 0)

The function f(x) is a polynomial function of 3rd degree, has a domain all real numbers and range all real numbers, its end behavior is rises at left and falls at right