Question

A fruit company guarantees that 87% of the pineapples it ships will ripen within four days of delivery. Find the probability that at least 10 pineapples in a case of 12 are ripe within four days. The probability is about _____.

Answer 1

The problem can be solved using the Binomial Probability Formula:

`P(X)=(^n_X)\cdot p^X\cdot(1-p)^(n-X)`

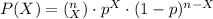
where X is the number of successes, n is the number of times an event can occur, and p is the probability of success.

From the question, we can get the following parameters:

`\begin{gathered} n=12 \\ p=87\%=0.87 \end{gathered}`

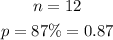
We can have that:

`P(X\ge10)=P(10)+P(11)+P(12)`

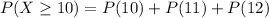
We have that:

`\begin{gathered} X=10 \\ P(10)=(^(12)_(10))\cdot0.87^(10)\cdot(1-0.87)^(12-10) \\ P(10)=(12!)/(10!(12-10)!)\cdot0.87^(10)\cdot(1-0.87)^(12-10) \\ P\mleft(10\mright)=0.2771 \end{gathered}`

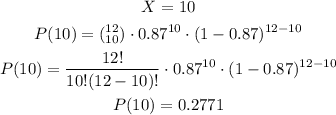
Using the steps above, we can calculate the other values to be:

`\begin{gathered} P(11)=0.3372 \\ P(12)=0.1880 \end{gathered}`

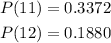
Therefore, the probability is calculated to be:

`\begin{gathered} P(X\ge10)=0.2771+0.3372+0.1880 \\ P(X\ge10)=0.8023 \end{gathered}`

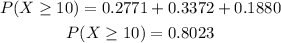
The probability is about 0.8023.