Given the following values (UNDER 25)
![\begin{gathered} \operatorname{mean}=\mu_1=8.5 \\ \text{standard deviation}=\sigma_1=68 \end{gathered}]()
Given the following values ( OVER 25)
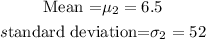
State the null and alternative hypothesis

State the significant level; alpha is 0.05
Calculate the statistical test
![t=\frac{\mu_1-\mu_2}{\sqrt[]{\frac{\sigma^2_1}{n_{}}+\frac{\sigma^2_2}{n_{}}}}](https://img.qammunity.org/2023/formulas/mathematics/college/hv1khu24ctv9r7vfbhmsclbozks6bv9h6v.png)
![\begin{gathered} \text{where n=16} \\ t=\frac{8.5-6.5}{\sqrt[]{(68^2)/(16)+(52^2)/(16)}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/irlqbmetfardmmagdq5v2o0icrt97zv7dd.png)
![t=\frac{2}{\sqrt[]{289+169}}=\frac{2}{\sqrt[]{458}}=(2)/(21.4)=0.093](https://img.qammunity.org/2023/formulas/mathematics/college/wbsaumkxlqtsel5gi94bhgi7y8az70ljhu.png)
The degree of freedom is
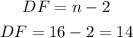
The P-value for the t-test score using a P-value calculator is 0.4636
Since the P-value is more than the alpha level, that is
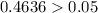
Hence, the null hypothesis is accepted and there is no significant difference between them