Question

Which graph represents the solution to the inequality y<
`(1)/(2)`-4?

Answer 1

Given the inequality:

`y\leq(1)/(2)x-4`

Let's graph the inequality.

Apply the slope-intercept form:

y = mx + b

Where m is the slope and b is the y-intercept.

From the inequality given, we have:

slope = ½

y-intercept = -4

Let's graph the inequality using 3 points.

• When x = 2

`\begin{gathered} y\leq(1)/(2)(2)-4 \\ \\ y\leq1-4 \\ \\ y\leq-3 \end{gathered}`

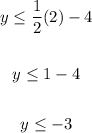
• When x = -2

`\begin{gathered} y\leq(1)/(2)(-2)-4 \\ \\ y\leq-1-4 \\ \\ y\leq-5 \end{gathered}`

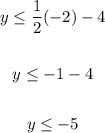
Therefore, we have the points:

(0, -4)

(2, -3)

(-2, -5)

Mark the points on the line then draw