First, let's sketch the problem with the forces acting on the book:
1)
Since the book remains motionless, the sum of forces is equal to zero, in the 15° direction (table surface) and in the direction perpendicular to the table.
In the table direction, we have the frictional force and a component of the weight force:
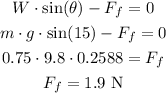
The frictional force is equal to 1.9 N.
2)
In the perpendicular direction, we have:
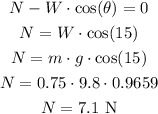
The normal force is equal to 7.1 N.