We have
Quarter =.25
Nickel= =.05
x= number of quarters
y= number of nickels
the first equation is
x+y=20
The second equation is
.25x+ 0.05y=2.60
Then we solve the system of equation , with the first equation we isolate the x
x=20-y
then we substitute the equation above in the second equation
.25(20-y)+ 0.05y=2.60
We sum similar terms
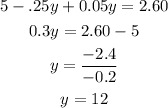
we substitute the value of y in the equation with x isolate
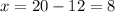
therefore the answer is
8 quarters and 12 nickels