Question

Which of the following models could be used to find two numbers whose sum is 221, but whose product is a maximum?

Answer 1

Let's call x and y to the unknown numbers. Their addition must be equal to 221, then:

x + y = 221

Isolating y, we get:

y = 221 - x

The product of these numbers is:

`\begin{gathered} f(x)=x\cdot y \\ f(x)=x(221-x) \\ \text{ Distributing:} \\ f(x)=221x-x^2 \\ Or \\ f\mleft(x\mright)=-x^2+221x \end{gathered}`

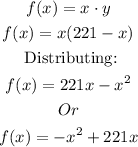
In this function, the leading coefficient is negative (-1), then the quadratic function has a maximum.