Question

Sketch the graph of a parabola using the given information:

Answer 1

Given:

Range is

`y\ge0`

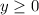
Vertex is (0,0).

Required:

To sketch the graph of a parabola.

Step-by-step explanation:

The general equation of the parabola is,

`y=a(x-h)^2+k`

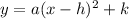
Where (h,k) are the vertex.

Now,

`\begin{gathered} y=a(x-0)^2+0 \\ y=ax^2 \end{gathered}`

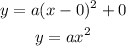
Here the range is positive.

Consider the parabola function

`y=x^2`

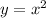
No matter what real number value the x and y cannot be a negative number, because a square number always greater than or equal to zero.

In this case we can say that the range of the parabola function is greater than or equal to zero ( y>=0).

Now the graph of the function is,

Final Answer:

The graph of the function is,