Question

What is the domain of h?h(x)=6 square root (4x+3) over (9x-4)

Answer 1

Given the function:

`h(x)=\frac{6\sqrt[]{4x+3}}{9x-4}`

Let's find the domain of the function.

The domain of a function is the possible values of x which makes the function true.

To find the domain of the function, set the denominator to zero and solve for x.

We have:

9x - 4 = 0

Add 4 to both sides:

9x - 4 + 4 = 0 + 4

9x = 4

Divide both sides of the equation by 9:

`\begin{gathered} (9x)/(9)=(4)/(9) \\ \\ x=(4)/(9) \end{gathered}`

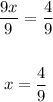
Also, set the expression in the radicand greater or equal to zero and solve for x.

4x + 3 ≥ 0

Subtract 3 from both sides:

4x + 3 - 3 ≥ 0 - 3

4x ≥ -3

Divide both sides by 4:

`\begin{gathered} (4x)/(4)\ge-(3)/(4) \\ \\ x\ge-(3)/(4) \end{gathered}`

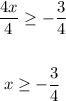
The domain of h is:

`\mleft\lbrace x\vert x\ge-(3)/(4),x\\e(4)/(9)\mright\rbrace`

Therefore, the domain of h in interval notation is:

`\lbrack-(3)/(4),(4)/(9))\cup((4)/(9),\infty)`