Question

the number of female members of congress has increased approximately linearly from 85 members in 2005 to 108 members in 2015. Let n be the number of female members of congress at t years since 2005.

Answer 1

a) n = 2.3t + 85

b) Female members will be betwen 121 to 122

Step-by-step explanation:

In 2005, members = 85

In 2015, members = 108

n = number of members since 2015

t = time since year 2005

t = 0 (base year), n= 85

t for 2015:

t = 2015 - 2005

t = 10, n = 108

We need to find the rate of increase:

`\begin{gathered} \text{rate = }\frac{change\text{ in number of members}}{\text{change in year}}\text{ = }\frac{change\text{ in n}}{\text{change in t}} \\ \text{rate = }\frac{108\text{ - 85}}{10\text{ - 0}} \\ \text{rate = }(23)/(10) \\ \text{rate = }2.3 \end{gathered}`

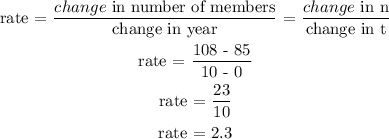
We need to find of the linear model using equation of line:

y = mx + b

In this case, y = n, x = t

m = rate = 2.3

We need to find b.

b = is the number of members when t = 0

b = 85

The equation or linear model becomes:

`\begin{gathered} n\text{ = mt + 8}5 \\ n\text{ = 2.3t + 8}5 \end{gathered}`

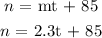
b) The number of female members in 2021 = ?

year = 2021

t = 2021 - 2005

t = 16

We substite for t in the linear model:

`\begin{gathered} n\text{ = 2.3t + 85} \\ n\text{ = 2.3(16) + 85} \\ n\text{ = 36.8 + 85} \\ n\text{ = 121.8 members} \end{gathered}`

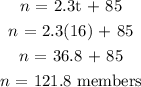
Since we can't have a decimal number of people, females members will be at least 121 members or at most 122 members