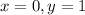Answer: We need to construct a table for the given function, and then graph it and answer all the remaining parts:
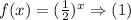
(a) The table for function (1) Is as follows:
The plot is as follows:
(B) Domain of the function:
The domin of the function can be determined by inspecting the graph, therefore the domain is as follows:
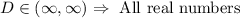
(C) Range of the function is:
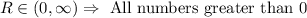
(D) Equation of the asymptote.
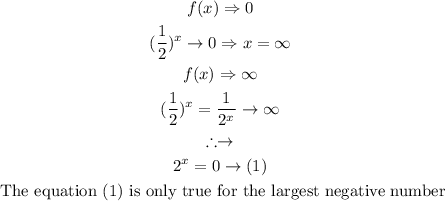
(E) Y-intercept: