Question

I need help with this problem I need to write an equation for the proportional relationship

Answer 1

Proportionality

The table shows the cost in dollars (c) for different weights of apples (w).

If the cost and the weight are proportional, then their ratio must be constant for all the values of the tables, that is:

`(c_1)/(w_1)=(c_2)/(w_2)=(c_3)/(w_3)\ldots`

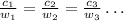
Let's test the ratio for each row of the table:

`(\$3.76)/(2)=\$1.88`

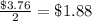
This represents the cost of 1 pound of apples.

`(\$5.64)/(3)=\$1.88`
`(\$7.52)/(4)=\$1.88`
`(\$9.40)/(5)=\$1.88`

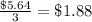
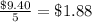
Because all of the ratios are equal we can conclude that the cost of apples is proportional to the weight of apples

The equation that relates cost (c) and weight (w) is:

c = 1.88w