Given the figure shown in the picture, you can identify that there is a circle inside a square. Therefore, the area of the shaded region can be calculated by subtracting the area of the circle from the area of the square.
The formula for calculating the area of a circle is:
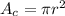
Where "r" is the radius of the circle.
The formula for calculating the area of a square is:
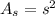
Where "s" is the side length of the square.
Therefore, you can write the following formula for calculating the area of the shaded region:
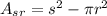
In this case, you can identify that:
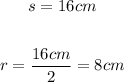
Therefore, by substituting values into the formula and evaluating, you get:
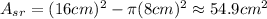
Hence, the answer is: Last option.