Given:
A tree stump considering a right cylinder.
The circumference of the right cylinder, C=209 inches.
The volume of the right cylinder, V=33370 cubic inches.
Required:
We need to find the height of the stump in feet.
Step-by-step explanation:
The base of the right cylinder is a circle.
Consider the formula to find the circumference of the circle.
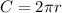
Substitute C = 209 in the formula.

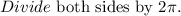
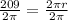
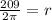

Consider the formula to find the volume of the right cylinder.
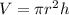
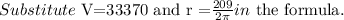
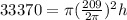
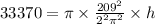
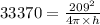
Solve for h.

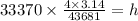
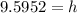

We know that 1 foot = 12 inches.
Divide the height by 12 to get convert from inches to feet.
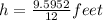
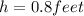
Final answer:
The height of the stump is 0.8 feet.