Answer:
(8,2)
Step-by-step explanation:
Given the system of inequalities:
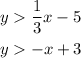
First, we determine the x and y-intercepts of each inequality to plot the boundary line.

Since we have the greater than sign, shade above the boundary line.
For the second inequality:

Since we have the greater than sign, shade above the boundary line.
Any point in the region where the two graphs intersect (shaded purple) is a solution to the system of inequalities.
• One point is (8,2).
You can pick as many points as possible.