Question

Two forces are applied to a car in an effort to move it, as shown in the figure below. (Let F1 = 440 N and F2 = 370 N. Assume up and to the right are in the positive directions.)An illustration shows an overhead view of a car as it approaches a fork in the road. The car is oriented such that it is directed toward the top of the illustration. A force F1 extends from the nose of the car and points along the left-side forked road at an angle of 10° measured counterclockwise from the car's initial direction. A force F2 extends from the nose of the car and points along the right-side forked road at an angle of 30° measured clockwise from the car's initial direction.(a) What is the resultant vector of these two forces?magnitude _____Ndirection _____ ° to the right of the forward direction(b) If the car has a mass of 3,000 kg, what acceleration does it have? Ignore friction._____ m/s2

Answer 1

Given:

The magnitude of force F1 is: F1 = 440 N

The magnitude of force F2 is: F2 = 370 N

The angle that force F1 makes with the car's initial direction is: θ₁ = 10° Counterclockwise

The angle that force F2 makes with the car's initial direction is: θ₂ = 30° Clockwise

To find:

a) The magnitude and the direction of the resultant vector of these two forces.

b) The acceleration of the car.

To find:

a)

The following diagram indicates the components of the forces acting on the car.

The resultant force acting in the up direction is:

`F_y=F_1cos\theta_1+F_2cos\theta_2`

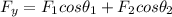
Substituting the values in the above equation, we get:

`\begin{gathered} F_y=440\text{ N}* cos10\degree+370\text{ N}* cos30\degree \\ \\ F_y=440\text{ N}*0.9848+370\text{ N}*0.8660 \\ \\ F_y=753.732\text{ N }j \end{gathered}`

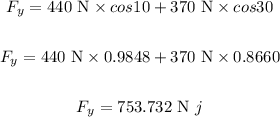
The resultant force acting in the up direction is 753.732 Newtons. j in the above equation represents the up direction of the force.

The resultant force in the right/left direction is:

`F_x=-F_1sin\theta_1+F_2sin\theta_2`

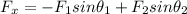
Substituting the values in the above equation, we get:

`\begin{gathered} F_x=-440\text{ N}* sin10\degree+370\text{ N}* sin30\degree \\ \\ F_x=-440\text{ N}*0.1736+370\text{ N}*0.5 \\ \\ F_x=108.616\text{ N }i \end{gathered}`

The resultant force acting in the right direction is 108.616 Newtons. i in the above equation represents the right direction of the force.

Now, the total resultant force is given as:

`\begin{gathered} F=F_x+F_y \\ \\ F=108.616\text{ N }i+753.732\text{ N }j \end{gathered}`

Now, the magnitude of the resultant force is calculated as:

`\begin{gathered} |F|=√(108.616^2+753.732^2) \\ \\ |F|=761.517\text{ N} \\ \\ |F|\approx761.52\text{ N} \end{gathered}`

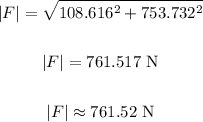
Thus, the magnitude of the resultant force is 761.52 Newtons.

Now, the direction of the resultant force (to the right of the up/forward direction) can be determined as:

`\begin{gathered} tan\theta=(|F_x|)/(|F_y|) \\ \\ \theta=tan^(-1)((\lvert F_(x)\rvert)/(\lvert F_(y)\rvert)) \end{gathered}`

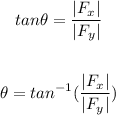
Substituting the values in the above equation, we get:

`\begin{gathered} \theta=tan^(-1)((108.616)/(753.732)) \\ \\ \theta=tan^(-1)(0.1441) \\ \\ \theta=8.19\degree \\ \\ \theta\approx8.2\degree \end{gathered}`

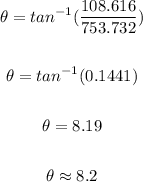
The direction of the resultant force is 8.2° from the up/forward direction of the initial motion of the car.

b)

By using Newton's second law of motion, the acceleration of the car can be calculated as:

`\begin{gathered} |F|=ma \\ \\ a=(|F|)/(m) \end{gathered}`

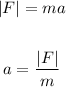
Substituting the values in the above equation, we get:

`\begin{gathered} a=\frac{761.52\text{ N}}{3000\text{ kg}} \\ \\ a=0.2538\text{ m/s}^2 \end{gathered}`

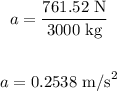
The acceleration of the car in the direction of the resultant force is 0.2538 m/s².

Final answer:

a) The magnitude of the resultant force is 761.52 Newtons in the directio of 8.2° from the up/forward direction of the initial motion of the car.

b) The acceleration of the car is 0.2358 m/s².