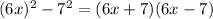Question

Factor the expression. 36x^2−49

Answer 1

`(6x+7)(6x-7)`

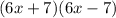
Step-by-step explanation:

Given the below expression;

`36x^2-49^{}`

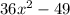
Since both terms are perfect squares, we can rewrite the above expression as;

`(6x)^2-7^2`

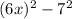
We can now apply the below difference of squares formula;

`a^2-b^2=(a+b)(a-b)`

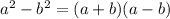
If we compare the above formula with our expression, we can see that a = 6x and b = 7.

Let's go ahead and substitute;

`(6x)^2-7^2=(6x+7)(6x-7)`