Let s be the speed of the slowest train and t the time it takes to travel 300 miles.
We know that:

Since the second train has a speed of s+20 mph and travels the same 300 miles using 4 hours less time, then:
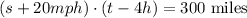
Isolate t from the first equation:
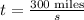
Substitute the expression for t in the second equation to find an expression only in terms of s:
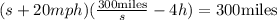
Use the distributive property to rewrite the product of the quantities on the left hand side of the equation:

Simplify the products when possible. 4h times 20 mph is equal to 80 miles:

Substract 300 miles from both sides of the equation:
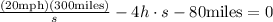
Multiply both sides by s:
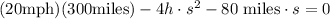
This is a quadratic equation for s. Write the equation in standard form:

Use the quadratic formula to isolate s:
![s=\frac{80\text{ miles}\pm\sqrt[]{(80\text{ miles})^2-4(-4h)(20mph)(300miles)}}{2(-4h)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/415bj6sxfmv8msyqph5h4oho893i5a55iq.png)
Observe that the term -4(-4h)(20mph)(300miles) is equal to +96000 squared miles, and 80 miles squared is equal to 6400 squared miles:
![s=\frac{80\text{ miles}\pm\sqrt[]{6400+96000}\text{ miles}}{-8h}](https://img.qammunity.org/2023/formulas/mathematics/high-school/4w76e5fus66ej2td5av14t2rzouakqjeft.png)
Factoring out the units, we get:
![s=\frac{80\pm\sqrt[]{102400}}{-8}\text{ mph}](https://img.qammunity.org/2023/formulas/mathematics/high-school/5elrveg7zy8extx9akn0ks4anr8zfv4ope.png)
Since the square root of 102400 is equal to 320:

Taking the positive value of the plus/minus sign, we get:
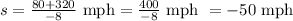
Taking the negative value of the plus/minus sign, we get:
Since we first stated that s*t=300 miles and the time cannot be a negative number, the only acceptable answer is s=30 mph.
Since the velocity of the second train is s+20 mph and s=30mph, then the velocity of the second train is 50 mph.
Check the answer by verifying if all the conditions are satisfied. The problem says that the second train arrives 4 hours earlier.
The first train takes a time of 300 miles / 30 mph = 10 h.
The second train takes a time of 300 miles / 50 mph = 6h, 4 hours earlier.
Therefore, the velocities of the trains are 30 mph and 50 mph.