Answer:
x=2, y=-7
Step-by-step explanation:
Given the system of equations:
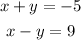
To solve the system by elimination, we add the two equations to eliminate y.
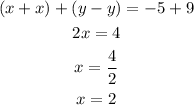
Next, we substitute x=2 in any of the equations to solve for y.

The solution to the system of equations is therefore: (2, -7).