To solve for the interest, the formula is:
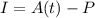
where A(t) is the accumulated value after t years and P = the initial money.
Since we do not have A(t) given in the question, we have to solve it first. The formula for compounding annually is:
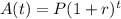
where A(t) is the accumulated value after t years, P = the initial money, r = rate of compounding in decimal form, and t = time in years.
In the question, P = $130, r = 9.4% or 0.094 in decimal form, and t = 2 years. Let's plug these values into the formula above to solve for the maturity value of the money.
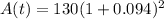
1. Add the numbers inside the parenthesis first (1 + 0.094).
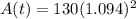
2. Apply the exponent on 1.094 → (1.094 x 1.094).
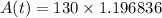
3. Lastly, multiply the initial money 130 to the result in step 2.
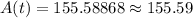
Hence, after 2 years, the money will become $155.59.
So, the interest is:
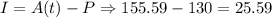
The initial money will have accumulated interest of $25.59 after 2 years.