Question

Find four consecutive integers whose sum is 270.Select one:a.67, 68, 69, 70b. 66, 67, 68, 69c.65, 66, 67, 68d.66, 68, 70, 72

Answer 1

You have to find 4 consecutive integers whose sum is 270.

Let "x" represent the first integer.

The next one can be expressed as (x+1)

The third one can be expressed as (x+2)

The fourth one can be expressed as (x+3)

The sum of these integers must be 270 so that:

`x+(x+1)+(x+2)+(x+3)=270`

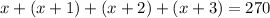
From this expression, you can determine the value of x:

- First, order the like terms together and simplify:

`\begin{gathered} x+(x+1)+(x+2)+(x+3)=270 \\ x+x+1+x+2+x+3=270 \\ x+x+x+x+1+2+3=270 \\ 4x+6=270 \end{gathered}`

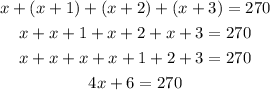
-Second, subtract 6 to both sides of the equal sign to pass the term to the right side of the expression:

`\begin{gathered} 4x+6-6=270-6 \\ 4x=264 \end{gathered}`

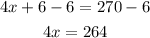
-Third, divide both sides by 4 to determine the value of x:

`\begin{gathered} (4x)/(4)=(264)/(4) \\ x=66 \end{gathered}`

Now that you know the value of the first integer, you can determine the other three:

`\begin{gathered} x=66 \\ x+1=66+1=67 \\ x+2=66+2=68 \\ x+3=66+3=69 \end{gathered}`

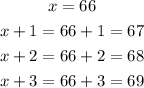
The four consecutive integers that sum 270 are 66, 67, 68, and 69. (option b)