Sum and Product of the Roots of a Quadratic Equation
Given a quadratic equation of the form:
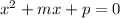
It can be proven that (-m) coincides with the sum of the roots of the polynomial and p corresponds with the product of the roots.
For example, a polynomial with roots 3 and 4 has the equation:
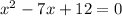
We are given the equation:
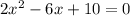
Notice the coefficient of the x squared is not 1 as required. But we can do the trick of dividing by 2:
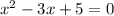
Now we can say:
The sum of the roots is 3
The product of the roots is 5