Question

Hi can somebody help me with this statistics question ?S=28.2

Answer 1

The bell-shaped distribution is the normal distribution. To label the curve, you have to apply the empirical rule of the normal distribution.

Remember that the mean is always in the center of the distribution.

This rule states that:

68% of the distribution is within 1 standard deviation of the mean of the distribution.

95% of the distribution is within 2 standard deviations of the mean of the distribution.

99.7% of the distribution is within 3 standard deviations of the mean.

In the graph you can write this rule as follows:

The given distribution has the following statistics:

`\begin{gathered} Mean\colon\bar{x}=143 \\ S\tan dard_{\text{ }}Deviation\colon S=28.2 \end{gathered}`

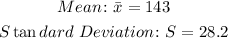
• The distribution has its center at the mean, in this case, the center of the distribution is 143.

• 68% of the distribution will be within 1 standard deviation of the mean, you can determine the values as follows:

`\begin{gathered} \bar{x}\pm S\to143\pm28.2 \\ 143+28.2=171.2 \\ 143-28.2=114.8 \end{gathered}`

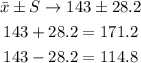
68% of this distribution is within 114.8 and 171.2.

• 95% of the distribution is within 2 standard deviations of the mean, that is:

`\begin{gathered} \bar{x}\pm2S\to143\pm2\cdot28.2=143\pm56.4 \\ 143+56.4=199.4 \\ 143-56.4=86.6 \end{gathered}`

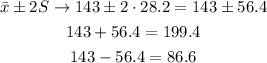
95% of this distribution is within 86.6 and 199.4.

• 99.7% of the distribution is within 3 standard deviations of the mean, that is:

`\begin{gathered} \bar{x}\pm3S\to143\pm3\cdot28.2=143\pm84.6 \\ 143+84.6=227.6 \\ 143-84.6=58.4 \end{gathered}`

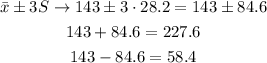
99.7% of this distribution is within 58.4 and 227.6.

Next, you have to draw the intervals calculated: