The quadratic is
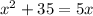
Subtract 5x from both sides
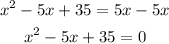
To solve it we will use the formula
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
a is the coefficient of x^2
b is the coefficient of x
c is the numerical term
Since a = 1, b = -5, c = 35
Then substitute them in the formula above
![x=\frac{-(-5)\pm\sqrt[]{(-5)^2-4(1)(35)}}{2(1)}](https://img.qammunity.org/2023/formulas/mathematics/college/9eilr5jx70bz6lsidqoxev3n7x8ffxc4c6.png)
Simplify it
![\begin{gathered} x=\frac{5\pm\sqrt[]{25-140}}{2} \\ x=\frac{5\pm\sqrt[]{-115}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7me3xdgcrf8etx15nz6wnlc84f9xqxnn8g.png)
since the square root of a -ve number is imaginary, then we will use i
![\begin{gathered} x=\frac{5\pm\sqrt[]{115}.\sqrt[]{-1}}{2} \\ x=\frac{5\pm\sqrt[]{115}i}{2} \\ \sqrt[]{-1}=i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gekq4fi3ofiisqvhhpz6fopxq9nhtqlj8p.png)
The solutions are
![\mleft\lbrace\frac{5+\sqrt[]{115}i}{2},\frac{5-\sqrt[]{115}i}{2}\mright\rbrace](https://img.qammunity.org/2023/formulas/mathematics/college/d3amzjgixxpuk1a0kflmgc0qi6olb6orzx.png)