Given the following system of equations:
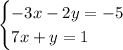
notice that we can multiply by 2 the second equation to get:
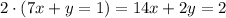
then, we can add both equations to get the following:
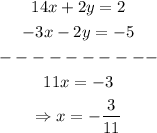
Now that we have that x=-3/11, we can use this value to find y on the original second equation:
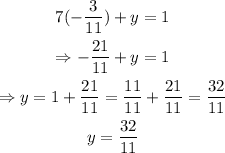
therefore, the solution of the syste is (-3/11,32/11)