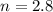Given:
g(n) varies inversely with n
so,
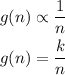
Where (k) is the proportionality constant
We will find the value of (k) using the given condition
When n = 2, g(n) = 11
Substitute with n and g(n)
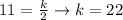
So, the relation between g(n) and (n) will be:
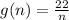
We will find the value of (n) when g(n) = 8
So, substitute with g(n):
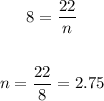
Rounding the answer to the nearest tenth
so, the answer will be: