Answer:
Account 2 is better because the profit is $41.40, about $2.07 more than the profit for Account 1.
Explanation:
For account 1:
Principal, P = $800
Time, t = 1 year
Number of times interest is compounded per year, n = 365
Interest rate, r = 4.8% = 4.8/100
r = 0.048
Amount in account 1 after 1 year is:
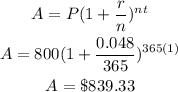
The interest = $839.33 - $800
The interest on account 1 = $39.33

ROI on account 1 = 4.9%
For account 2:
Principal, P = $810
Time, t = 2 year
Number of times interest is compounded per year, n = 4
Interest rate, r = 2.5% = 2.5/100
r = 0.025
Amount in account 1 after 1 year is:
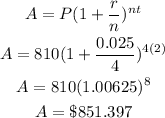
The interest = Amount - Principal
The interest = $851.397 - 810
The interest(Profit) on account 2 = $41.397

ROI on account 2 = 5.1%
Account 2 is better because the profit is $41.40, about $2.07 more than the profit for Account 1.