Question

In the right triangle with 30' acute angle the long leg is 12 ft. Find other sides and the area of the triangle

Answer 1

We have the following:

In this case the first thing is to calculate the value of the hypotenuse, by means of the cosine function.

`\begin{gathered} \cos \theta=\frac{\text{adjacent}}{\text{hypotenuse}} \\ \theta=30 \\ \text{adjacent = 12} \end{gathered}`

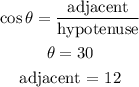
replacing:

`\begin{gathered} \cos 30=\frac{12}{\text{hypotenuse}} \\ \text{hypotenuse}=12\cdot\cos 30=13.86 \end{gathered}`

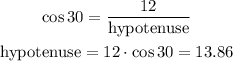
now, to calculate the side we use the Pythagorean theorem, as follows

`\begin{gathered} c^2=a^2+b^2 \\ 13.86^2=12^2+b^2 \\ b^2=13.86-12^2 \\ b=6.94 \end{gathered}`

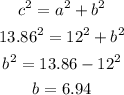
Therefore, the area is:

`\begin{gathered} A=(12\cdot6.94)/(2) \\ A=41.64 \end{gathered}`

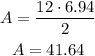
The area is 41.64 ft^2