Given that the area of a rectangular patio is 105 ft².
The length of the patio is 8 ft longer than the width of the patio.
The equation is
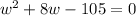
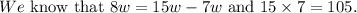
The given equation can be written as follows.
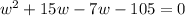
Taking out the common terms.
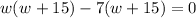
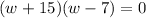
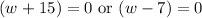
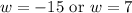
The measure can not be negative.
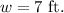
Hence the width of the patio is 7 ft.
Option D is correct.