Question

confused on how to answer this question! i need help, any help this is part of a homework practice exercise

Answer 1

We have that 20% of the women biopsed have breast cancer. If the sample size is 200,000, then we have that:

`(200,000)(0.2)=40,000`

then, there are 40,000 women with breast cancer.

Next, we have that the test is positive for approximately 2% of the women that don't have breast cancer. Then, if the remaining 160,000 women of the sample don't have breast cancer, we have that:

`160,000(0.02)=3200`

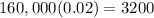
we also have that the test is negative for the 5% that do have breast cancer, then we have:

`40,000(0.05)=2000`

With this information we can fill the hypothetical frequence table:

Finally, to calculate the probability that a woman does not have breast cancer given that the test is negative, we can use conditional probability to find out:

`\begin{gathered} P(no\text BC \frac{P(no\text{ BC and test-)}}{P(test\text{ -)}} \\ =((156000)/(200000))/((158800)/(200000))=(156000)/(158800)=0.98 \end{gathered}`

therefore , the probability is 0.98 = 98%