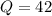Q varies inversely as the square of p and q =36 when p =7. Find Q when p =6

Question

asked Mar 15, 2023 156k views

1 Answer

Wdetac · Answer 1 · 2023-03-19T13:27:34+0000

Answer:

The value of Q when p=6 is;

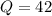
Step-by-step explanation:

Given that Q varies inversely as the square of p;

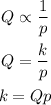
$\begin{gathered} Q\propto(1)/(p) \\ Q=(k)/(p) \\ k=Qp \end{gathered}$

Where k is the constant of proportionality.

Given;

Q =36 when p =7.

Let's substitute the given values to determine the value of k;

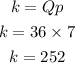
$\begin{gathered} k=Qp \\ k=36*7 \\ k=252 \end{gathered}$

So, when p =6, Q will be;

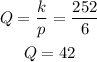
$\begin{gathered} Q=(k)/(p)=(252)/(6) \\ Q=42 \end{gathered}$

Therefore, the value of Q when p=6 is;