Question

cach x value into the equation and sobre for todo and then write the equation using the rolet Instructions: 1. Complete Lesson Practice Part II on pas 2. Show all work 3. Upload the assignment 7) Find the slope using the slope forma identify the y-intercept, substitute the zi - aimes nto y=mx+b

Answer 1

hi,

first, we have to find the coefficient m (slope):

`m=(Y2-Y1)/(X2-X1)`

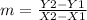
For that, we can choose two points that intersects this line:

I will use (0, -4) and (6,0).

`m=(0-(-4))/(6-0)=(4)/(6)=(2)/(3)`

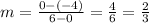
So, the slope (m) = 2/3.

Now, we have to find the value of b (linear coefficient):

`y=\text{ mx +b}`

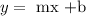
Again, lets select another point. I will use when y = 0. Point (6,0):

`\begin{gathered} y=\text{ mx +b} \\ 0\text{ = }(2)/(3)\cdot6\text{ + b} \\ 0\text{ = }4\text{ + b} \\ -4\text{ = b} \end{gathered}`

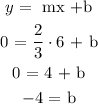
So, we can say that Y interception is equal to -4. Another mode to solve that, you can look at the image and select the point where X =0, so the other coordinate will be the intersection.

Your answer is:

slope: 2/3

y-intersection: -4