Question

HELP ASAPThe graph given is a function of f. 5 3 2 -5 -4 -3 -2 -1 2 3 4 5 -1 -2 -3 -4 1. (lph Find (-1) 2. Cipt Find f'(-3) 3. (pt) Find f'(1) 4. (1pb Describe what it means to find the inverse of a given value. Use complete sentences.

Answer 1

If we have a function y=f(x), this means that for an input x we get an output that is y.

If g is the inverse function of f, then x=g(y). This means that when the input is y we get x.

We can write this as:

`f(a)=b\longrightarrow f^(-1)(b)=a`

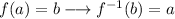
The relation is reciprocal, so if g is the inverse of f, then f is also the inverse of g.

Then, if we have to find f^-1(-1), we have to find the output when the input is -1. That is the same as finding the input of f when the output is -1.

We can look this in the graph as:

We identify the output y=-1 and then we find that f(1)=-1, so the input is x=1. Then, we can write:

`f(1)=-1\Rightarrow f^(-1)(-1)=1`

We can repeat the process for f^-1(-3) and f^-1(1):

Then, we have:

`\begin{gathered} f(1.5)=-3\Rightarrow f^(-1)(-3)=1.5 \\ f(-1)=1\Rightarrow f^(-1)(1)=-1 \end{gathered}`

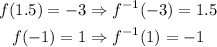
Answer:

1) f^-1(-1) = 1

2) f^-1(-3) = 1.5

3) f^(1) = -1

4) The inverse function inverts the relation between input and output of a function. If the function gives a certain output y for a certain input x, its inverse function will give output x for the input y.